STATISTICAL MECHANICS         PHYS 222

 

Fall 2002                                 Homework #1                         Dr. P. Misra

                                                Due     09/06/02

 

 

 

1.                  Two identical bodies have equations of state U = NCT, with C a constant. The values of N and C are the same for each system. The initial temperatures are T₁ and T₂, and they are to be used as a source of work by bringing them to a common final temperature T_f.

 

(a)    What is the range of possible final temperatures?

 

(b)   What final temperature corresponds to the maximum amount of delivered work, and what is this maximum amount of delivered work?

 

 

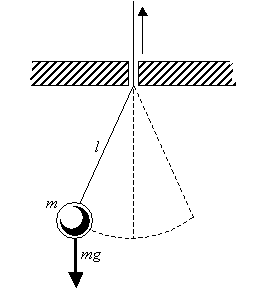
2.                  As illustrated in the figure below, a string with a lead ball of mass m is slowly pulled upward through a small hole. Consider the work done on the system during this process. Find the change in energy and the frequency of this pendulum during this “adiabatic process”, assuming the amplitude of the pendulum to be small.

3.   Prove on the basis of the principle of entropy increase that, when a coordinate x varies extremely slowly through a quasi-static adiabatic process, the entropy S(x) does not change. (Hint: Consider dS/dt as a function of dx/dt and recall that a quasi-static adiabatic process in statistical mechanics is one involving a very slow change of a parameter x which determines a purely mechanical interaction of a system with an external work source.)