STATISTICAL MECHANICS         PHYS 222

Fall 2002

Homework #3

Due      09/18/02

Dr. P. Misra

1.                              Define .  Show that  at .  Use numerical integration to calculate .  (Useful in Planck’s law of radiation).  (Exact answer is )

2.                              We wish to calculate vapor pressure of water at 20°C more accurately.

(a)    Heat capacity of water is 1 cal/(g°C).  Heat capacity of water vapor (steam) is 0.35 cal/(g°C).  What is the latent heat at 20°C?

(b)   Use the average latent heat to calculate the vapor pressure of water at 20°C.

3.                              Assuming constant C_V, calculate the entropy S of one mole of Van der Waals gas for a given volume V and temperature T.  Show that your result is identical to the eqn.  (for ideal gas) when a = 0 and b = 0.

4.                              Assuming constant C_V, what is the equation for the PV-curve for the adiabatic process of a van der Waals gas?  Show that your result is identical to the eqn.   (for ideal gas) when a = 0 and b = 0.

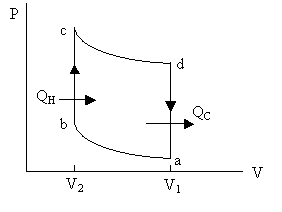
Fig. 1.  Otto cycle for automobile engine.  ab and cd are adiabatic processes.  bc and da are constant volume processes.  Q_H is the heat from the burning gasoline.  Q_C is the waste heat out of the exhaust pipe.  (H=hot, C=cold)

5.                              The automobile gasoline engine can be approximated by the Otto cycle shown as Fig. 1.  For the intake and compression strokes ab, air-gasoline mixture is compressed adiabatically from V₁ to V₂.  For the power stroke, gasoline burns to produce energy Q_H (bc at constant volume V₂) and then expands adiabatically (along the path cd) from V₂ to V₁.  For the exhaust stroke da, waste gas and the waste heat Q_C goes out of the tailpipe at the constant volume V₂.  The compression ratio R of the engine is defined as R = V₂/V₁.  Assuming ideal gas behavior, show that the efficiency of the engine is (Q_H – Q_C) / Q_H = 1–R^g-1, where g = C_P/C_V is defined by the eqn. g = 1+(R/C_V) and R < 1.
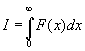