STATISTICAL MECHANICS         PHYS 222

Spring 2002

Homework #4

Due      09/20/02

Dr. P. Misra

1. Consider a gas that undergoes an adiabatic expansion from a region of constant pressure p_i and initial volume V_i to a region with constant pressure p_f and final volume V_f (as shown in the figure below).

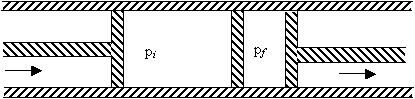
(a)    By considering the work done by the gas in the above throttling process, find the initial and final enthalpies of the gas and the relationship between them.

(b)   What can be said about the intermediate states of the system?

(c)    Calculate the temperature difference (ΔT) between the two regions for a small pressure difference Δp = p_f - p_i.

(d)   Using the above result, discuss the possibility of using the process to cool either an ideal gas, or a more realistic gas obeying the equation

p (V-b) = RT. Explain your result.

2. A Carnot cycle is operated using a liquid-gas interface as shown below. The vapor pressure is p_v, the temperature and volume are T and V, respectively. The cycle is operated according to the p-V diagram shown.

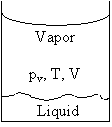
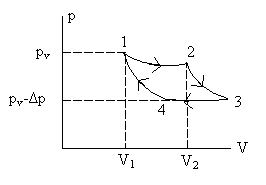
The thermodynamic cycle progresses isothermally from state 1 to state 2, evaporating n moles of liquid. This is followed by reversible cooling from 2 to 3, and subsequently a contraction from 3 to 4, which results in condensation of n moles of liquid. Finally, a reversible heating of the system from 4 to 1 completes the cycle.

(a)    Noting that V₂ – V₁ = V_g – V_l, where V_g = volume of n moles of gas and V_l = volume of n moles of liquid, calculate the efficiency in terms of Δp, V_g – V_l, and the latent heat L_v of vaporization of a mole of liquid.

(b)   Use the result of part (a) to obtain an expression for dp_v/dT in terms of (V_g – V_l), n, L_v and T.