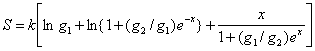Statistical Mechanics
		PHYS 222
Dr. P. Misra
Fall 2002		Homework #6	Due: 10/18/02
1.	Consider a monatomic crystal consisting of N atoms. These may be situated in two kinds of positions: a. Normal position, indicated by 0 b. Interstitial position, indicated by X Suppose that there is an equal number (=N) of both kinds of position, but that the energy of an atom at an interstitial position is larger by an amount ε than of an atom at a normal position. At T=0 all atoms will therefore be in normal position. Show that, at a temperature T, the number n of atoms at interstitial sites is for n << N Use the fact that the Helmholtz free energy is a minimum for equilibrium at constant volume and temperature
2.	Consider a two level system with eigenstates |1ñ and |2ñ having, respectively, energies ε1 and ε2, and ε2 > ε3. a. if the system is in the state |yñ = a|1ñ + b|2ñ, what is the density matrix ρ? b. Let the system be in thermal equilibrium at temperature T. What is ρ? What is F? What is S?
3.	The quantum states available to a given physical system are (i) a group of g1 equally likely states with a common energy value ε1 and (ii) a group of g2 equally likely states, with a common energy value ε2. Show that the entropy of the system is given by where p1 and p2 are, respectively, the probabilities of the system being in a state belonging to group 1 or to group 2: p1+ p2 = 1. a. Assuming that the p’s are given by a canonical distribution, show that where x = (ε2-ε1)/kT, assumed positive. b. Verify the foregoing expression for S by deriving it from the partition function of the system. c. Check that as T→0, S→k ln g1. Interpret this result physically.